#28 - Premium Appraisal Models for NFT Markets
Introducing First-Principles Valuation Models for Enhanced Interpretability
Stanford Blockchain Review
Volume 3, Article No. 8
📚Authors: Yusen Zhan PhD, Black, Tony Ling – NFTGo
🌟 Technical Prerequisite: Advanced
Introduction
Within the constantly-evolving landscape of Non-Fungible Tokens (NFTs) [3], effective pricing models need to strike a balance between complexity and interpretability. Take, for instance, the commonly used metric of a “floor price” in NFT trading. We see that in many cases, although the floor price reflects a rough starting point and baseline metric, it usually does not accurately mirror an NFT’s intrinsic value or features [2].
Historically, many NFT pricing models have relied on Gradient Boosted Decision Trees (GBDT), which, while offering reliable predictions, are extremely complex and hard to interpret [1][4]. In this article, we introduce a new “Premium Appraisal Model” for NFT pricing, aimed at creating a novel valuation model that takes into account the market’s foundational structures and first principles. Through capturing these far more nuanced features of NFTs, we hope to allow creators, traders, and collectors in the NFT space to better navigate the complexities of NFT pricing.
Baseline: Gradient-Based Decision Tree Models
At present, one common model technique for NFT pricing is Gradient Boosted Decision Trees, or GBDT. This ensemble learning method evolves from the foundational principle of decision trees, wherein individual trees discern decisions based on set criteria. However, what sets GBDT apart is its sequential construction of multiple trees. With each new tree built, it aims to rectify the mistakes of the preceding one, incrementally enhancing the accuracy of the ensemble. This systematic, iterative methodology equips GBDT models with the capability to discern and integrate intricate data patterns and subtle nuances.
Strengths of GBDT Models
Robustness: GBDTs are resilient to outliers in the dataset, making them suitable for diverse data scenarios.
Handling Mixed Data: GBDTs can seamlessly manage datasets that contain a mix of categorical and numerical features.
Automatic Feature Selection: The nature of the model allows it to prioritize and select relevant features, often reducing the need for extensive feature engineering.
Reduced Overfitting: Due to the ensemble nature and the iterative corrections, GBDTs generally exhibit less overfitting compared to individual decision trees.
Challenges and Limitations of GBDT Models:
Complexity: As an ensemble of multiple trees, understanding the inner workings or tracing a specific decision path in GBDT can be intricate.
Training Time: GBDTs, due to their iterative nature, often require more training time than simpler models.
Memory Intensive: Storing multiple decision trees demands significant memory, which can be a limitation in resource-constrained environments.
Complexity and Lack of Transparency: The Core Issue
The most pronounced challenge with GBDTs in the context of our NFT pricing is the lack of transparency. While the model might provide a price or a valuation, it is a “black-box” algorithm that cannot simply explain why it arrives at a given price.
The very strength of GBDTs, their ability to capture minute data patterns across multiple trees, becomes a double-edged sword when we need to justify or explain a pricing decision to stakeholders. This lack of clear interpretability, results in pricing metrics that are hard to fathom to the various stakeholders in the NFT space. Thus, this underscores the importance of offering a pricing model that offers both accuracy and explainability.
Overview of the Premium Model for Strategic NFT Pricing
As established above, we are introducing a Premium Model for NFT pricing, one which balances accuracy with explainability by aligning prices with foundational principles and traits of these digital assets.
A NFT pricing consists of collection-based value and its trait premiums
The core formula underpinning the Premium Model is expressed as:
Here:
Estimate Price: The predicted value of the NFT.
Floor Price: The lowest price at which an NFT is currently listed for sale in a particular collection or category on the market.
Intercept: This could be considered as a base adjustment to the floor price, accounting for intrinsic factors that might universally adjust prices up or down across a given NFT collection or market.
Trait Weights: These are the coefficients that are assigned to each trait to determine how much that trait influences the price of an NFT. Each trait contributes proportionally to the estimated price based on how it is valued relative to the floor price.
Trait Premiums: Additional values attributed to particular, desirable traits or characteristics of the NFT. They are the product of the Floor Price and their corresponding Trait Weights.
Collection-based Value: This represents the baseline value of an NFT within a collection, derived from the floor price and potentially influenced by an intercept that accounts for general market conditions or other factors not tied to specific traits. Mathematically, it can be represented as:
Derivation of the Premium Appraisal Model
Within the Premium Model, we use linear regression to analyze how specific traits influence the estimated price of an NFT. With trait weights and the floor price acting as the variables, the linear regression model can effectively predict the price of an NFT, according to its inherent traits and the current market baseline.
According to our Premium Model, we have
After a simple transformation, it yields
Renaming the left-hand side to y, and the right-hand side to linear regression form, we get:
Where
yis the predicted outputxis a one-hot encoded vector representing the traits of an NFT. Each position in the vector represents a specific trait, and the vector is "hot" (i.e., set to 1) at the position corresponding to the trait(s) the NFT has, and zero otherwise.wis a weight vector, where each element represents the weight associated with a specific trait in determining the NFT’s price.bis the intercept, adjusting the prediction independently of the traits.
The wT * x term is computed as the dot product of the two vectors, which is:
In a practical use-case, suppose you have 3 traits (A, B, C). An NFT with traits B and C would be represented by the one-hot vector x = [0, 1, 1]. The linear regression model predicts the NFT’s price based on the learned weights for each trait and the intercept so that we can rewrite the sum of Trait Weights as wTx. We can implement the linear regression model using open-source machine learning libraries to build our premium model based on the above analysis [7].
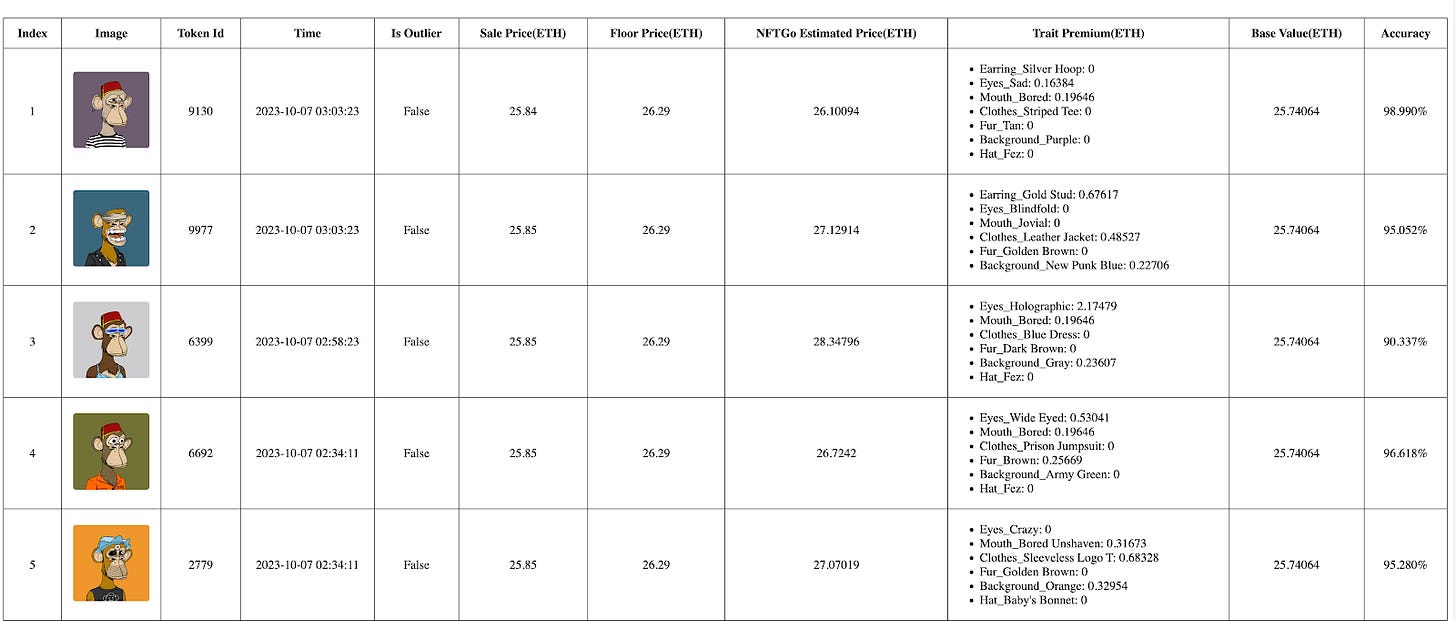
Appraisal Demonstration
We can use our premium pricing model for the rare Bored Ape Yacht Club #7403. Following is the basic information corresponding to this token:
This token possesses various traits, encompassing Trippy Fur, Faux Hawk Hat, Angry Eyes, Aquamarine Background, Silver Hoop Earring, and Phoneme Mouth. Among these, Trippy Fur is identified as the most rare attribute. According to our GoPricing API, #7403 has the following appraisal results:
The "pricing" is the estimated price for token 7403, which is 104.42672366856866 ETH, and the "floor" is the Floor Price at the requested time. Our estimated price can be decomposed as:
From the above example, we just need to calculate the premiums instead of weights and show the final estimated result to users, as shown in the following demo:
Advantages of the Premium Appraisal Model
Given the above theoretical derivation and practical demonstration of the Premium Appraisal Model, we can see how this provides a framework for practical and market-aligned pricing strategies. This in turns allows for a pragmatic, adaptive, and transparent valuation approach. We can summarize some of the key features and advantages of the Premium Appraisal Model as follows:
Linearity: The Premium Model preserves a linear relationship with the floor price, maintaining consistent price ratios among NFTs and traits, contingent upon a determined set of weights.
Transparency: A standout feature is the model’s inherent transparency, as the parameters are not only easy to validate but also offer clear visibility into the valuation process.
Real-Time Responsiveness: The model embodies a real-time nature, where an NFT’s price is reflexive to alterations in the floor price, ensuring that valuations are consistently in sync with prevailing market dynamics.
Credible Neutrality: Eschewing third-party biases such as rarity perception or sentimental value, the parameters are deduced through a linear average, grounded strictly in transaction history and utilizing only sale price and floor price as inputs during training.
Interpretability:
Clarity in Parameters: Each parameter, whether it’s weights or intercept, is infused with tangible meaning, elucidating trait importance and collection base value within the NFT space.
Shared Trait Weights: Analogous to how traits permeate through different NFTs, trait weights are cohesively shared across various NFT prices, ensuring a unified and consistent valuation approach.
Thus, the Premium Model balances simplicity and complexity to ensure transparency in the ever-changing world of NFTs. By focusing on clarity, adaptability, and fairness, it provides a strong foundation for valuing NFTs accurately and effectively.
Conclusion
Pricing models are crucial in the fast-paced NFT marketplace, where transparency is highly valued. While tree-based models like GBDT have been popular, their complexity can pose challenges. To address this, there's a shift towards more transparent linear premium models.
Looking ahead, we expect to integrate premium models with NFT Pricing Oracles, Lending Protocols, and Automated Market Makers (AMMs). For instance, in NFT Pricing Oracles like Chainlink, premium models can refine pricing inputs, ensuring more stable pricing feeds. In NFT Lending Protocols such as BendDAO, advanced pricing models can facilitate secure NFT-collateralized loans, opening up new avenues for NFTs in DeFi.
Additionally, in AMMs for NFTs like Uniswap v4, advanced pricing models could enhance swapping algorithms, aligning rewards with NFT value and rarity. Beyond this, premium models could navigate fractionalized NFT ownership, shape NFT indices, and drive the evolution of synthetic NFTs, all while maintaining robust, transparent, and user-friendly pricing mechanisms across NFT platforms and financial applications.
About the Authors
Yusen Zhan
Yusen Zhan is a senior lead AI engineer at NFTGo. Previously, he worked at Grab and Alibaba Inc. as a Machine Learning lead. Yusen has a PhD in Computer Science from Washington State University. He is also an NFT OG since 2018 and collects many blue-chip NFTs like BAYC, AZUKI, DEGODS.
Black
Black is a researcher and developer focusing on the innovation of NFTs. He had several years of experience in machine learning and natural language processing before entering crypto space.
Tony Ling
Tony Ling is the co-founder of NFTGo. He has been an early member of the Stanford Blockchain Club since 2018. Additionally, he authored a paper titled "A Bitcoin Valuation Model Assuming Equilibrium of Miners’ Market Based on Derivative Pricing Theory" (2019) and has delivered speeches and participated in panels worldwide.
References
[1] Hastie, T., Tibshirani, R., & Friedman, J. H. (2009). Boosting and Additive Trees. In The Elements of Statistical Learning (2nd ed., pp. 337-384). Springer. https://doi.org/ISBN: 978-0-387-84857-0
[2] Chainlink. NFT Floor Price. Retrieved from https://docs.chain.link/data-feeds/nft-floor-price
[3] William Entriken (@fulldecent), Dieter Shirley, Jacob Evans, & Nastassia Sachs. (2018). ERC-721: Non-Fungible Token Standard. Ethereum Improvement Proposals, no. 721. Retrieved from https://eips.ethereum.org/EIPS/eip-721
[4] NFTGO. NFTGO Pricing. Retrieved from https://docs.nftgo.io/docs/gopricing
[5] BendDAO. BendDAO Portal. Retrieved from https://docs.benddao.xyz/portal/
[6] Uniswap Labs. Uniswap v4. Retrieved from https://blog.uniswap.org/uniswap-v4
[7] Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., ... & Vanderplas, J. (2011). Scikit-learn: Machine learning in Python. Journal of machine learning research, 12(Oct), 2825-2830.