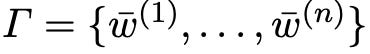#53 - Cryptography Research Spotlight: BPR Traitor Tracing for Threshold Decryption

A Conversation with Dan Boneh

Stanford Blockchain Club

Oct 16, 2024

Stanford Blockchain Review
Volume 6, Article No. 3

📚 Interview Guest: Dan Boneh – Stanford University

Article by Jay Yu and Yavor Litchev – Stanford Blockchain Club

🌟 Technical Prerequisite: Advanced

Introduction

Threshold decryption is a flexible yet powerful tool that allows for secure management of trusted secrets by distributing key shares among multiple parties. However, current threshold decryption systems are not robust against cases where participants may choose to sell their decryption key shares to an adversary.

In this article, we will dive into “Accountability for Misbehavior in Threshold Decryption via Threshold Traitor Tracing”, a new paper by Stanford Professor Dan Boneh’s Applied Cryptography Group that addresses this problem. First, we will explore the overarching idea of threshold decryption and its features. We do this to motivate why accountability measures are necessary for threshold decryption schemes in the first place. Next, we will examine the overall construction of Boneh, Partap, and Rotem’s novel traitor tracing scheme, which we term BPR Traitor Tracing. Finally, we discuss the applications and implications of BPR Traitor Tracing on threshold decryption in the blockchain space.

Threshold Decryption

Threshold decryption is an instance of multi-user cryptography. In a threshold decryption setup, there is a public key that anyone can use to encrypt data. On the other hand, decrypting data requires a secret decryption key that is shared amongst N different parties. To decrypt a piece of data, there needs to be a quorum of at least t parties to decrypt a ciphertext using a “threshold signature.” Importantly, t - 1 or less parties cannot learn anything about the plaintext from the ciphertext. This construction is called a t-out-of-N threshold decryption scheme, which often creates shards of the keys and distributes said shards to each of the participants using techniques such as Shamir’s secret sharing algorithm [1].

In many respects, a t-out-of-N threshold signature scheme is like a traditional “multi-signature wallet” (multisig) such as a Gnosis Safe wallet. A multisig also requires a quorum of t-out-of-N signatures to take any action, such as transferring funds to another user or casting a ballot for a proposal. However, a threshold signature scheme has many desirable properties and holds several advantages over a traditional multisig.

Firstly, a traditional multisig requires all t members to sign, so the number of signatures needed scales linearly to t. For a 9-out-of-12 multisig, such as for Arbitrum’s security council [2], this would require verifying 9 signed messages for a multisig action. In a threshold signature setup, on the other hand, this would only require verification of a single signature, composed of 9 out of the 12 signature shards. Therefore, it is much cheaper and easier to scale threshold signature setups than multisigs.

Secondly, the shards of a threshold signature can undergo a process of proactive refresh [3], where the key shards themselves can be updated at regular intervals. This means that even if an attacker compromises a user’s key shards, the user can simply refresh their key shards, and the old shards that the attacker has become invalid. This process of proactive refresh is impossible to do in a traditional multisig setup. If an attacker compromises the secret key of one of Arbitrum’s security council members, it will have signing access to that account in perpetuity. The multisig would need to laboriously revoke the compromised users’ signature through a group vote. Therefore, a threshold signature setup has a significant security advantage over a traditional multisig.

Thirdly, in multisig wallets, all of the t signees are public. If Alice, Bob and Charlotte are three members of a security council, in a multisig setup, everyone can publicly view how they each individually voted on each proposal. This is great in some cases as an accountability measure to ensure that signees act in good faith. In other cases, however, it may be desirable to not reveal who specifically voted for what – such as in contentious proposals with risk of retaliation. Threshold schemes can help alleviate this accountability problem by ensuring that the final produced signature is identical no matter which parties participated in the signing process, thus granting plausible deniability to the participants.

Threshold signatures come in two flavors that provide for both options. Accountable threshold signatures identify the specific shards (users) that participated in generating the threshold signature, just like a classic multisig. Private threshold signatures, on the other hand, do not reveal either the signees that participated in the generation of the signature, nor the threshold itself [1]. Thus an attacker does not even know how many shares it needs to forge a signature.

Although private threshold signatures can allow an organization to preserve their internal structure and not reveal this to the outside world, there is an accountability problem with private threshold signatures. Specifically, if an attacker has a general idea of who the signees are for the private threshold signature, they can bribe each of the signees for their shards. Once the attacker gains t shards, they’re able to decrypt any given ciphertext from the comfort of their home.

BPR Traitor Tracing for Private Threshold Signatures

Because by nature, a private threshold signature is “private” and does not reveal which shards generated this signature, it is impossible to trace which signees sold their signatures. This is a huge problem, as it means that standard accountability mechanisms, such as slashing bad actors, would not work in a private threshold signature setup. This is precisely the problem that BPR Traitor Tracing seeks to tackle [4].

To better understand how such a tracing algorithm can be created, we must first formulate what we wish to accomplish with such tracing. Intuitively, we wish to be able to detect a set of participants in the decryption process, and make sure that we do not falsely identify and accuse innocent parties.

To formalize this notion, given a set of decrypting participants J, if the traitor tracing algorithm identifies a subset of parties J’, it is critical that J’ is a subset of J. In other words, it should be of negligible probability that any of the parties identified in J’ are not in fact involved in the actual decryption parties J. This would appear to be a sufficiently robust definition for what we seek to accomplish with traitor tracing, however the following issue arises: The traitor tracing algorithm that always outputs none of the parties (i.e. J’ is the empty set) will perfectly satisfy this definition. This is clearly unacceptable, as we would wish to have this tracing algorithm to be practically useful in identifying at least one participant in the decryption process. Thus, we additionally require that J’ is never the empty set. Following this, we define Good Trace (GoodTr) and Bad Trace (BadTr) as follows [5]:

As we expect, under this definition our traitor tracing algorithm will always return a good trace, with cryptographically-small margin of error. Now that we have formalized our end goal, we need to first introduce a cryptographic primitive before we fully solve the problem of traitor tracing, and that is the idea of fingerprinting codes [5].

Formally, a binary fingerprinting code is a set of words:

where each w̅ is an ℓ-bit string.

A fingerprinting code comes with a function Trace. In this function, the adversary has access to a subset W ⊆ Γ of words. The adversary generates a new word w̅ by combining bits from words in W, such that for every n-th bit in w̅, it has to take the value of the n-th bit in an existing w in W. So if W = {011, 010, 001}, such that all w in W start with the “0” bit, then the adversary’s w̅ must also have “0” as their starting bit. We can call this word feasible for W. This requirement of feasibility and resulting distribution of bits ensures that w̅ can be traced back to at least one word in W, to identify traitor parties.

Although this primitive provides a “tracing” capability we need in our threshold decryption scheme, it is not immediately obvious as to how this mechanism can be usefully implemented within the context of traitor tracing. We need to introduce another building block: Bipartite Threshold Key Encapsulation Mechanism, or BT-KEM [6].

The core innovation in BT-KEM is that instead of representing words as binary sequences (0's and 1's), we represent these as pairs of secret keys. Each pair corresponds to a bit, with a “left key" representing 0 and the “right key” representing 1. This approach allows us to trace the decryption process back to specific groups of participants, similar to how traditional fingerprinting codes work.

When a group of decryptors collaborates, they create a "traceable" word using these secret key pairs. This word can be linked back to the specific subset of parties involved in the decryption. This solves our problem of identifying groups attempting unauthorized decryption, as using only one key from each pair reveals information about which group is involved.

The BPR traitor tracing mechanism builds on BT-KEM to create the Traitor Tracing Threshold KEM (TTT-KEM) [7]. The key addition here is a Trace function. While fingerprinting codes theoretically allow us to identify specific subsets of parties attempting decryption, the Trace algorithm makes this practical by leveraging BT-KEM.

Here's how Trace works:

We feed carefully crafted invalid ciphertexts into the decoder (the decryption mechanism used by potential traitors).
Some of these ciphertexts have a valid left component and an invalid right component, while others are entirely invalid.
By analyzing how the decoder responds to these different inputs, we can determine individual "bits" of the fingerprinting code.
Using these bits, we apply fingerprinting code tracing algorithms to identify which set of parties were likely involved in the unauthorized decryption attempt.

This approach allows us to effectively trace and identify groups attempting unauthorized decryption, even when they try to conceal their identities.

*TTT-KEM Trace Function Pseudocode. Image Source [8].*

BPR Traitor Tracing in Blockchain Applications

BPR Threshold Decryption Traitor Tracing has enormous implications for the blockchain space, as this is a cryptographic scheme that solves the accountability system for any private threshold decryption system.

Today, one of the most prominent applications of BPR traitor tracing is in securing encrypted mempools. Threshold decryption is used in encrypted mempools, such as the case in Osmosis [9], in order to minimize the impact of Maximal Extractable Value (MEV) operations and other orderflow attacks. The core idea for threshold decryption is that each validator holds a decryption shard, and transactions require 2/3 of the validators to be decrypted – thus requiring the finality of the block before knowing the block’s contents.

The problem that emerges here is that a MEV searcher that wants to decrypt transactions early can simply bribe validators to sell a decryption algorithm with their key shards. With BPR traitor tracing, even if malicious validators sell a decryption algorithm derived from their combined key shares, that algorithm can still be traced to these individual validators’ shards. The network can then slash these validators’ stakes, thereby increasing the security of the system [4].

Other potential applications of threshold decryption include in private voting systems and sealed-bid auctions, where there is a need for data to be encrypted to ensure privacy. A DAO such as Arbitrum, for example, may choose to have a private ballot on a sensitive topic, such as treasury management or committee elections. The key shards could be split amongst its security council members, and they can only decrypt and view the results of the private ballot after the election is over. This measure can potentially prevent herding, apathy and some other centralizing forces common in DAOs [10].

For sealed-bid auction systems, threshold decryption may be used such that the results and winning bids of an auction are only revealed after the auction period is over. This process prevents players from seeing other bidders' prices in an effort to “outbid” them, such as the case of ConstitutionDAO [11].

In both of these cases, BPR Traitor Tracing is necessary for them to be effective, as it provides an extra measure of accountability and enforcement in cases where, for example, a security council member decides to sell their decryption shares to some malicious third party.

Conclusion

Fundamentally, threshold decryption as a construction yields numerous benefits over other multi-user cryptography schemes such as multi-signature wallets. In particular, accountable threshold signatures exceed multisigs in their flexibility, efficiency, and security, and may see increased adoption of threshold decryption setups as time goes on.

BPR Traitor Tracing seeks to extend the security and usability of the other flavor of threshold decryption – private threshold signatures. Through combining the tracing capability of fingerprinting codes and the BT-KEM construction, the TTT-KEM solution that the authors present elegantly solves the accountability problem of private threshold signatures. With this trace data, this allows private threshold decryption setups to be more useful and efficient in various blockchain applications – from encrypted mempools to private voting and auctions and beyond.

About the Interviewees

Prof. Dan Boneh

Professor Boneh heads the applied cryptography group and co-directs the computer security lab. Professor Boneh's research focuses on applications of cryptography to computer security. His work includes cryptosystems with novel properties, web security, security for mobile devices, and cryptanalysis. He is the author of over a hundred publications in the field and is a Packard and Alfred P. Sloan fellow. He is a recipient of the 2014 ACM prize and the 2013 Godel prize. In 2011 Dr. Boneh received the Ishii award for industry education innovation. Professor Boneh received his Ph.D from Princeton University and joined Stanford in 1997.

Yavor Litchev

Yavor is an undergrad at Stanford pursuing a degree in computer science with a focus on cybersecurity and cryptography. He has previously engaged in research projects relating to secure machine learning and digital signatures with more flexible access structures at MIT PRIMES. More recently, he is researching secure systems and program execution using software fault isolation through the CURIS program. He is currently the cryptography research lead for the Stanford Blockchain Club.

Jay Yu

Jay, or 0xFishylosopher, is an undergrad at Stanford pursuing a double major in Computer Science and Philosophy. He is President of the Stanford Blockchain Club and founder of the Stanford Blockchain Review. He researches designs for Decentralized Autonomous Organizations (DAOs) and blockchain governance with Stanford Law School faculty and as a Research Fellow for IC3. He also works on the investments team at Pantera Capital.