#22 - Moore’s Law for Zero Knowledge Proofs

Levers of Performance Gains, and Patterns for Value Accural in ZKPs

Stanford Blockchain Club

and

Roy Lu

Aug 23, 2023

Stanford Blockchain Review
Volume 3, Article No. 2

📚Author: Roy Lu – LongHash Ventures
🌟 Technical Prerequisite: Moderate

Cover Image: https://www.asml.com/en/news/stories/2022/moores-law-evolution

Introduction

In this article, I explore how ZK may change our lives beyond web3, discuss the levers for performance gains, posit a "Moore's Law in Zero-Knowledge", and identify patterns of value accrual.

Zero Knowledge is one of the most transformational technologies in web3 today that holds promises in scaling, identity, privacy and more. But current levels of performance preclude it from many of its potential use cases. As ZK technology continues to mature, however, I posit that there will be an exponential growth in ZK technology bringing it to serve wide ranging applications across web3 and traditional industries. In the same way that Moore’s Law postulated that chip transistor density would double every two years, I now posit a similar exponential law for Zero Knowledge Proofs, specifically that:

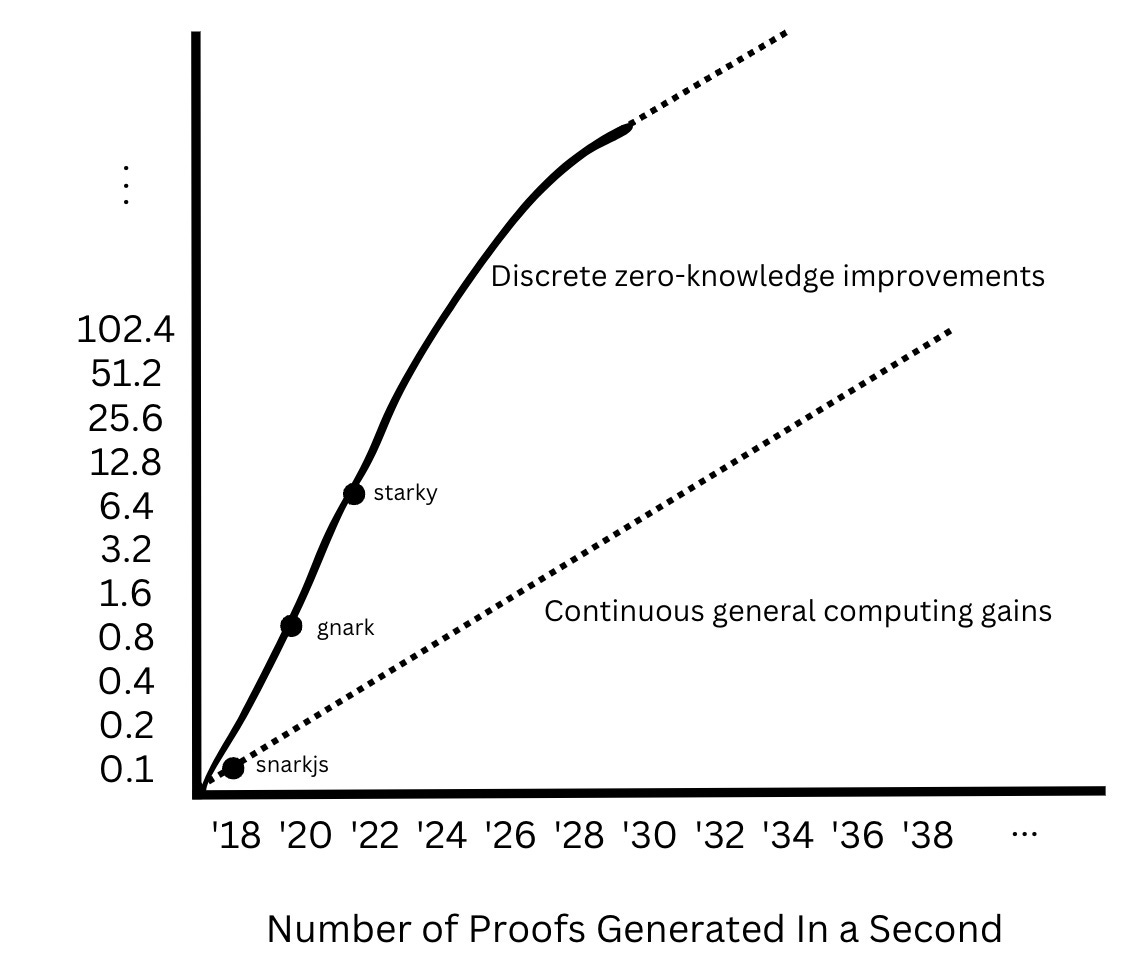
The number of proofs generated in a second will more than double over the next several years then asymptotically approach underlying general computing gains.

An Overview of Moore’s Law

Moore’s Law, a prediction made by Gordon Moore, co-founder of Intel, in 1965, posited “the complexity of semiconductor electronic integrated circuits will double every two years.” Over the past 58 years, Moore’s Law drove the advent of mobile computing, machine learning, and nearly every aspect of our digital lives, and in doing so, transforming the way we interact with technology.

Gordon Moore empirically observed that as the number of transistors doubled on a chip, the cost of manufacturing largely remained constant due to economies of scale. He further noticed that demand for computing power would drive investments into increasing transistor density.

As computational power enhanced exponentially on ever-smaller chips, this quantitative shift of transistor counts changed into a qualitative shift into how we use and interact with computers.

Our phones are more powerful computers than Apollo 11 that conveniently fit in our pockets and enables us to stream content from any site and communicate with anyone anywhere in the world. The training of large language models paved the release of ChatGPT that transformed the way we interact with information from data retrieval to intelligent synthesis.

Zero Knowledge Proofs and the Web3 Explosion

In the same way that the doubling of transistors and Moore’s Law enabled a qualitative shift in the way we interact with modern technology, Zero Knowledge Proofs’ exponential growth will unlock a new wave of novel application-layer experiences. At its essence, ZK bestows privacy, correctness, and scalability that are rooted in ZK’s properties of private computation, provable correctness, and recursive succinctness. These properties represent a fundamental shift towards a new computing paradigm.

Private Computation

Zero-knowledge allows computation to carry out on private modules with only the result to be shared and validated externally. As a real-world example, identity thefts can be prevented if banks adopt zero-knowledge computation. As an example, a user could allow a loan approval program to run on their identity information and credit history to get a loan approved without ever revealing their sensitive data to the bank — privacy is protected. In web3, ZK powers fully private L1’s such as Aleo and Mina or private payment networks such as Zcash, zk.money, Elusiv, and Nocturne. ZKP also allows teams like Renegade to run darkpools to list transaction orders without moving market prices. Value is transmitted without revealing a user’s private data.

Provable Correctness

For computations of opacity, zero-knowledge provides provenance to the input, output, and processing of the computation. An example is decentralized machine learning, where access to AI can be democratized through a network of remote compute nodes. ZKPs can attest to the data, weights, and training epochs in ML and prove that the entire training process was done as expected - correctness is established. In web3, zkML is already being implemented by teams like Gensyn, Modulus Labs, and general purpose ZKVMs such as Risc Zero. To prove the correctness of cross-chain states, ZKPs are used in ZK bridges such as Polymer, Succinct Labs, Herodotus, and Lagrange. ZK also enables applications such as Proven to attest to the correctness of reserves.

Recursive Succinctness

ZK can also collapse a stack of proofs into a single proof. Yet another real-world example is authenticity tracing in the supply chain. Manufacturers in each step of the supply chain can use ZKPs to prove the authenticity of its product without revealing sensitive manufacturing information. Then the ZKPs are recursively proved to generate a final ZKP that attests to the correctness of the entire supply chain - scalability is achieved. In web3, ZKPs for thousands of transactions can be rolled up into a single proof to power L2s such as Starkware, Scroll, and zkSync which drastically improve blockchain throughput.

Defining a Moore’s Law for ZK

From above, we’ve seen the abstract similarities between transistors enabling an application-level explosion, to ZKPs unlocking a similar wave of innovation in web3 innovation. Now it is time to derive a concrete definition of a “Moore’s Law for Zero Knowledge” through comparing general computation and ZK computation.

General Computing and Zero Knowledge Computing

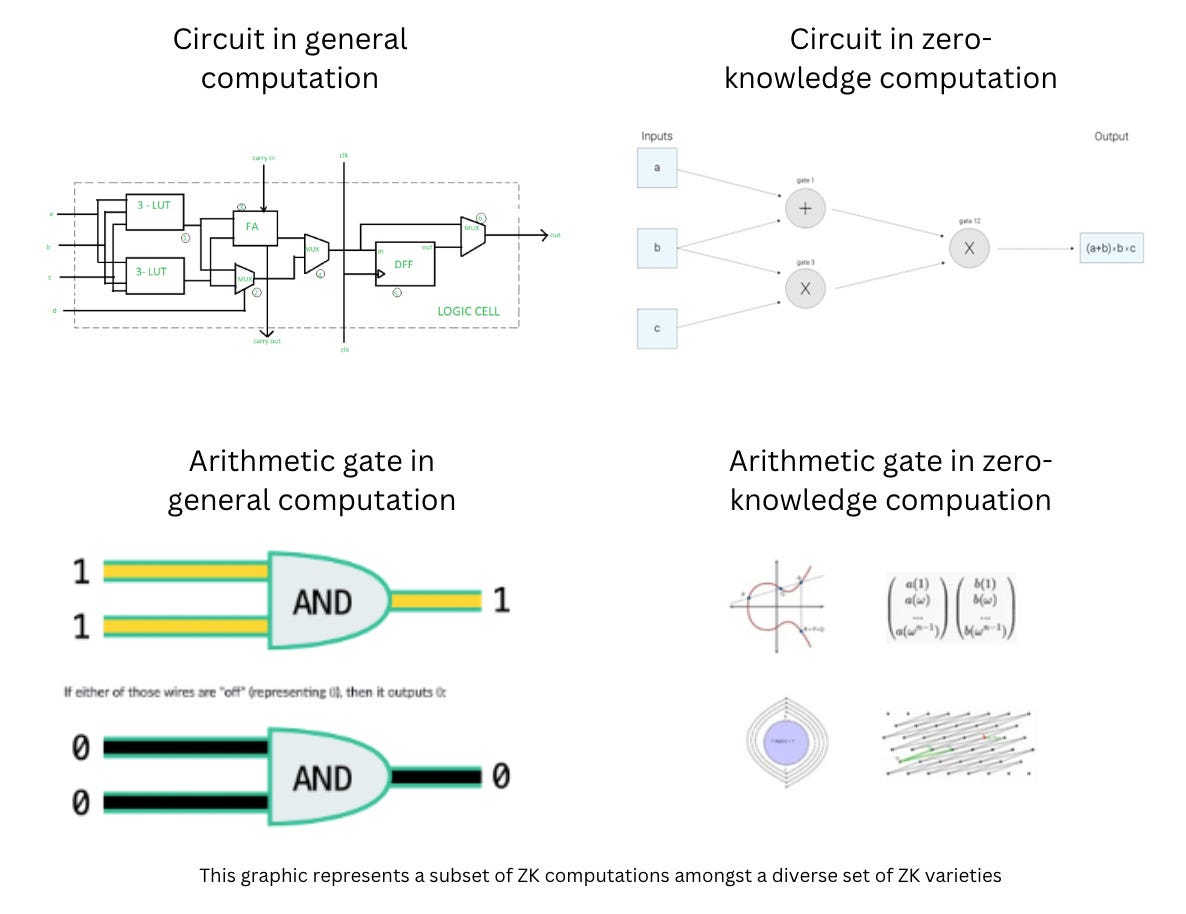
In general computing, gates consist of transistors that are metal-oxide silicon-based. Each gate can belong to one of several operands such as AND, OR, XOR, etc. Together, these operands enable programs to run.

All else held equal, zero-knowledge computation is more expensive than general computation. As an example, “hashing 10kb with SHA2 takes 140 seconds with Groth16, but takes just a few milliseconds without zero-knowledge.” This is due to the fact that ZK computation uses complex arithmetic for each operand.

In zero-knowledge computing, operands can be represented by finite fields. In the case of SNARKs, every operand is carried out on an elliptic curve [1]. In other variants of ZK, operands may consist of matrices, lattices [3], or modulos, which are also complex mathematical constructs for arithmetics [2]. Doing simple addition, subtraction, and multiplication is very costly using such operands. Data inputs are converted into finite fields instead of numbers. The complexity of these constructs is how cryptography derives its security. Although the arithmetic detail is beyond the scope of this article, the key takeaway is that in the same way that logic gates are executed on physical circuits, zero-knowledge logic is carried out in software circuits.

Thus, where physics governs performance gains in general computing, mathematics governs gains in zero-knowledge computing. Therefore, we recognize that Moore’s Law as applied to zero-knowledge exists in the software realm, not necessarily in the hardware realm, even though hardware acceleration also yields significant gains. From these fundamentals, we can also derive how a specific Moore’s Law in Zero Knowledge may look like.

Discontinuous Revolutionary Improvements in ZK

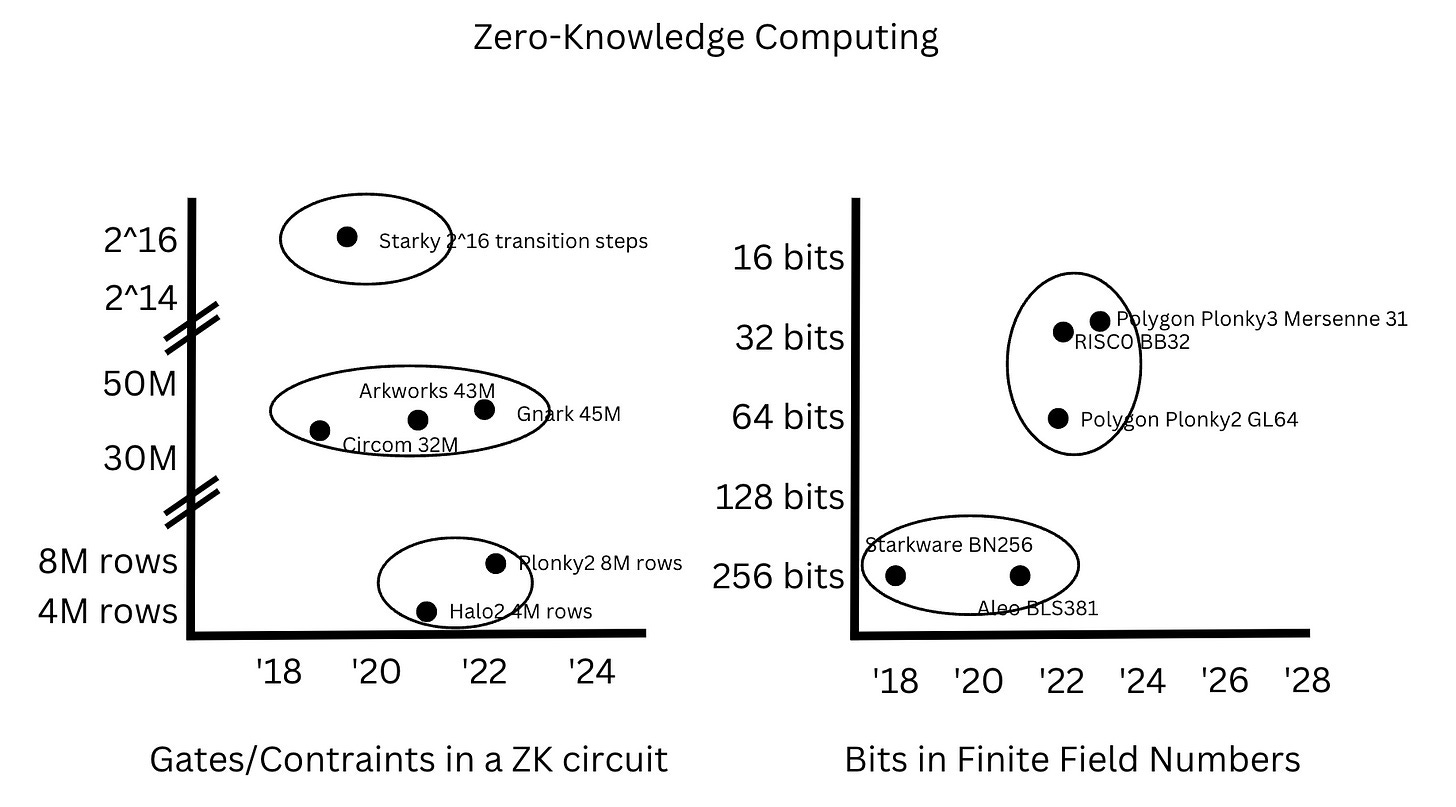
Perhaps the most important observation is that we find that while improvements in general computing occurred continuously, improvements in zk-computing take place in discrete steps.

Specifically, the number of cores in a CPU roughly doubled every five years from 2005 to 2020 and clock rates roughly doubled every five years from 1990’s to 2010’s. On the other hand, the number of constraints in a ZK circuits did not ‘improve’ continuously, but rather discretely jumped from 30-40M constraints in SNARKs, to 4-8M rows in PLONKs, then to 2^14-2^16 transition steps in STARKs [4]. By the same token, the number of bits in finite field numbers hovered around 256 bits from 2018 to 2022, then jumped to 32 bits between 2022 and 2023, in order to take advantage of 32-bit registers [5].

Further, recent development in HyperSpartan supports customizable constraint systems (CCS), to simultaneously capture R1CS, Plonkish, and AIR without overheads. And the introduction of SuperNova builds on Nova, a high-speed recursive proof system with folding schemes, that is compatible with different instruction sets and constraint systems. Both advances further broaden the ZK architectural design space

Based on these findings, a fundamental Moore’s Law in Zero-Knowledge would not be based on any single vector of continuous improvement, but rather an overarching performance gain measured in the number of proofs generated in a given amount of time, driven by discontinuous improvements. I posit that Moore’s Law in zero-knowledge will make discrete revolutionary jumps before inheriting from underlying general computing gains:

The number of proofs generated in a second will more than double over the next several years then asymptotically approach underlying general computing gains.

Reducing the Cost of Zero-Knowledge Proofs

As mentioned previously, Zero Knowledge Proofs in its current stage are far too brittle and expensive for a wide range of potential applications. In particular, the cost of verification far overshadows the cost of proof generation. A ballpark estimation of ZKP generation cost is <$1 USD, given that that 1) a 16 CPU 32GB memory EC2 on AWS costs $0.4/hr, with expectations that decentralized compute nodes would come at even lower costs, and 2) Polygon Hermez costs $4-6/hr generating about 20 proofs per hour.

However, the on-chain cost of verification remains burdensome at 230,000-5,000,000 gas per verification, which roughly translates to $100-2,000 per verification [8, 9]. While ZK rollups benefit from economies of scale by spreading the cost across thousands of transactions, other types of ZK applications must find ways to lower their verification costs, in order to realize the previously mentioned innovation on the application layer that will bring quality-of-life improvements to the end user.

Given that breakthroughs in ZK proof capacity will likely occur in disjointed and discrete steps, let’s examine the potential fronts where these breakthroughs may occur. Here are some of the potential optimizations listed in the zkprize:

Algorithmic optimizations that include MSM (multiscalar multiplication) and NTT (number-theoretic transformation) which are algorithms often applied to accelerate elliptic curve cryptography and themselves subject to hardware acceleration. Fourier transform is one example of NTT that’s been optimized in various implementations.
Parallel processing can increase the throughput of zero-knowledge by delegating parts of data structure preprocessing, circuit evaluations, or proof generation across multiple processing units or multiple threads.
Compiler optimizations that improve register allocation, loop optimization, memory optimization, and instruction scheduling.

In algorithmic optimization, an example is arithmetization moved from R1CS in SNARKS, to Plonkish in Halo2, Plonky2, and HyperPlonk, all of which are different from AIR used in Starky proofs [6]. Further, recent developments in Folding Schemes are exciting in that HyperNova can support incrementally verifiable computation with customizable constraint systems. In parallel processing, the Polygon team’s release of Plonky2 recursion widened the possibility of parallel proof generation [7]. In compiler optimization, the use of zk-friendly LLVM is interesting in that the IR (intermediate representation) can compile into opcodes agnostic of instruction sets. Examples are Nil Foundation’s ZK-LLVM and Risc0’s zkVM which also uses LLVM to produce ZKPs that trace every step of the execution. General ZKVM or LLVM extends zero-knowledge beyond blockchain use cases and increases code transferability for broader developer onboarding.

Implications for Zero-Knowledge Builders

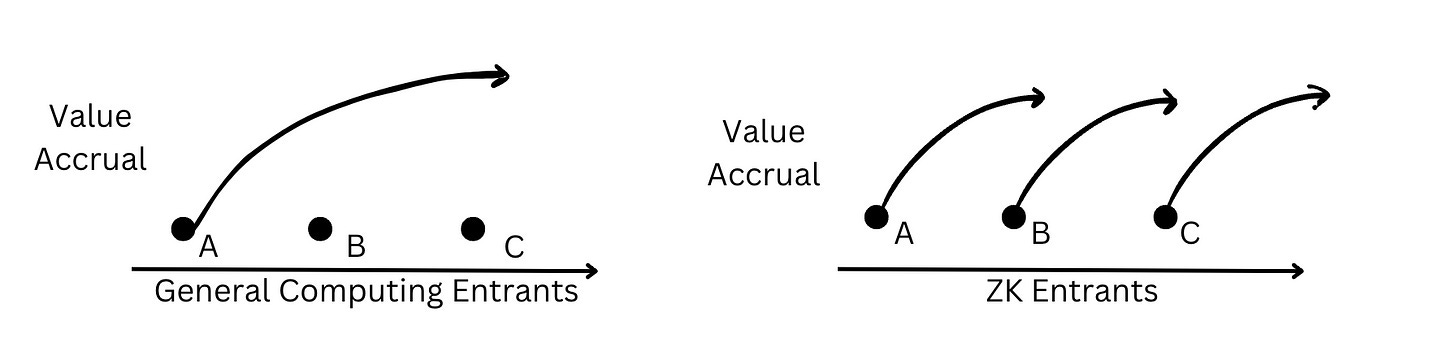
Value accrual in general computing generally favors the incumbent; chip manufacturers, for example, benefit from moats around costly capital investments that support incremental manufacturing improvements to produce ever-smaller chips. But since innovations in Zero-Knowledge happen in discrete revolutionary leaps, there is still ample opportunities for new teams to leapfrog incumbents through research-driven breakthroughs in technological capability, such as in the invention of new proof systems.

Based on this theory, there are a few takeaways for web3 zero-knowledge builders:

Zero-knowledge builders should consider modular designs. Where zk circuits are involved, protocol builders should consider modular designs that allow them to swap out ZK components for the most advanced ZK technology.
Entrants can benefit from research-driven disruption. For teams that have research capabilities, it is possible to come up with or be first-to-market to implement revolutionarily novel proof systems and leapfrog existing teams.
Vertical integrators can benefit from compositions of the newest tech. Because each layer in the zero-knowledge stack, from hardware to compilers to circuits, can undergo its own revolutionary improvement, vertical integrators can modularly adopt the newest tech and serve application teams the most advanced ZK tech at the lowest cost.

With this in mind, I anticipate three significant developments in the overall industry:

New teams leapfrogging current ZK protocols through technological breakthroughs
Existing protocols seeking ecosystem rather than technology-based moats
The emergence of vertically integrated ZK providers offering the latest tech at lower costs. Innovation and disruption lie ahead in this rapidly evolving landscape.

Conclusion

The oxymoron in technology is that when done right, the tech becomes invisible. We do not think about the cup when drinking water, any more than we pay attention to the computer chip when sending an email. A purpose is simply fulfilled, and we take the process for granted.

Zero Knowledge Proofs already hold the promise of delivering scalable applications with improved user experience. When done right, we won’t notice the proofs, but find our transactions more private, information more correct, and rollups faster and cheaper. As such, ZKPs may eventually weave into the fabric of our lives, in the same way that transistors, microchips, and now AI has found itself into our daily routine.

We won’t need to think about how zero-knowledge could prevent fraud during an election, how we save transaction costs by disintermediating middlemen from the financial system, or how AI training could become democratized because of decentralized computing using ZK. And perhaps one day, in the same way we enshrine Moore’s observation that “the number of transistors on a circuit board will double every 18-24 months” as a so-called “law,” we too, will take for granted that “the number of Zero Knowledge proofs per second will grow exponentially each year” while enjoying the fruits of these innovations. A purpose would be fulfilled, the hymn for ZK would be unsung, and we would carry on with our daily lives.

About the Author

Roy Lu is a Partner at LongHash Ventures and leads the firm's venture capital investments based out of SF. Roy had a non-linear path to venture capital. Prior to LongHash, he wore multiple hats - an AI founder, a hands-on full-stack engineer, and a dedicated biotech researcher. Believing in strong convictions and deep partnership with founders, Roy sees the transformative potential of web3 in forging an open, permissionless, and global economy. You can find more of his writing here.

Outside of the venture world, catch Roy hiking trails, exploring the latest culinary flights and tuning into deep house beats.